Building a Plain RSA PoC using Java
During a recent project as part of my studies, I developed a proof of concept (PoC) for plain RSA using Java. In this blog article, you will learn the mathematical principles behind RSA, along with a PoC implemented in Java code, uploaded to a dedicated GitHub Repository.
RSA Explained
RSA encryption is an asymmetric cryptographic algorithm based on the use of two different, yet mathematically related keys.
An RSA key pair consists of a public key and a private key. The public key is used to encrypt messages and can therefore be shared openly with others without posing a security risk. The private key, on the other hand, must remain confidential and is used to decrypt the encrypted data.
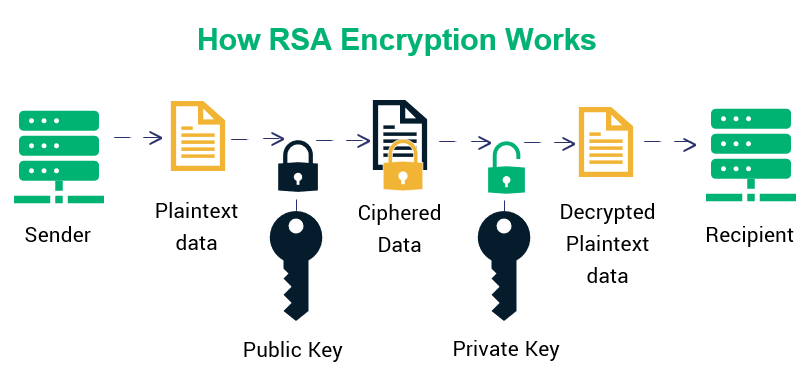
RSA encryption is hard to crack because its security relies on the difficulty of factoring a very large number into its two prime factors, a problem that is computationally infeasible for classical computers at sufficient key sizes. Without efficiently factoring that number, an attacker cannot derive the private key from the public key.
By clearly separating the public and private keys, the RSA algorithm enables both secure data transmission and the creation of digital signatures. In practice, RSA is commonly used in technologies such as TLS/HTTPS, email encryption, and systems designed to secure digital identities.
Mathematical Principiles of Plain RSA
First, two large prime numbers, usually p & q, are chosen. They are multiplied to create a modulus n that is used for both keys.
p ⋅ q = n
Next, the Euler’s totient (φ) value of n is calculated using the prime numbers choosen before. Euler’s totient function describes how many positive integers less than or equal to a given number are coprime to it.
φ(n) = (p – 1) ⋅ (q – 1)
After that, a public exponent e is selected that is compatible with φ(n) by satisfying the following mathematical conditions:
1 < e < φ(n)
hcf(e, φ(n)) = 1
*hcf = Highest Common Factor
Next, the private exponent d is calculated as the modular inverse of the public exponent. To solve this equation, the extended euclidean algorithm is beeing used.
d ≡ e⁻¹ mod φ(n)
Finally, the public key and the private key are formed.
Public Key = {e, n}
Private Key= {d, n}
To encrypt a message m into a ciphertext c, or the decrypt a ciphertext c to a message m, the following mathematical rules must be applied:
0 ≤ m < n
The keys can then be used to encrypt and decrypt messages by applying the corresponding encryption and decryption formulas.
Encryption: c = mᵉ mod n
Decryption: m = cᵈ mod n
Why is it called Plain RSA
Plain RSA refers to the direct application of the RSA mathematical formulas without any additional padding or randomized encoding schemes. In its early days, this straightforward approach was enough to demonstrate the underlying principles of RSA, which is why it is now commonly referred to as “plain” RSA in a more educational or theoretical context.
However, implementing plain RSA in production environments is considered insecure. Because the encryption process is fully deterministic, encrypting the same message with the same public key will always produce the same ciphertext. This makes plain RSA vulnerable to attacks such as ciphertext comparison, chosen-plaintext attacks, and message recovery for small or structured inputs. To mitigate these risks, modern implementations always combine RSA with secure padding schemes such as OAEP for encryption or PSS for signatures, which add randomness and significantly strengthen security.
Converting Messages into Decimal Numbers
As you may have noticed, we previously used the variable m to represent the message when calculating the ciphertext. However, most messages sent via email or text are not simple decimal numbers 😀. In order to encrypt a message using the RSA algorithm, it must first be converted.
Using the example message HELLO (where uppercase and lowercase letters are taken into account), each character is assigned its corresponding standardized ASCII decimal value. These decimal values are then converted into their respective binary representations:
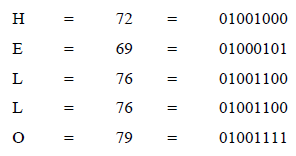
All of these binary values are then glued together in chronological order to form a single continuous binary sequence:
01001000 01000101 01001100 01001100 01001111
In the next step, this combined binary sequence is fully converted into a decimal representation. The resulting decimal value is therefore:
310400273487
The resulting decimal number can now be encrypted using the public RSA key. After the encrypted data has been transmitted, the recipient can decrypt it using the private RSA key. The decrypted decimal value can then be converted back into its original message form.
To do so, the decrypted decimal number is first transformed back into its corresponding binary representation.
01001000 01000101 01001100 01001100 01001111
The resulting binary number is then divided into 8-bit segments, commonly referred to as octets. Each of these 8-bit segments is subsequently converted into a decimal value and mapped back to its corresponding ASCII character.
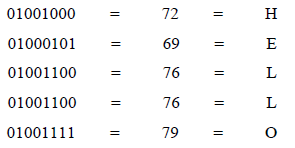
The result of this conversion is the original message, HELLO.
Builing a PoC using Java
Why Java?
Although I wouldn’t normally choose Java myself, its use was mandatory for this project as required by my university. Even though there is nothing wrong with Java, I personally would have chosen Python due to my prior experience with it and its overall simplicity.
GitHub
Feel free to check out & test the complete code in the GitHub repository I created.
Structure / “Main”
The main function first checks whether a “Files” directory exists in the user’s working directory and creates it if necessary. Next, it enters a continuous menu loop where the user can choose to generate a RSA key pair, create a message, encrypt a message, or decrypt a message.
Generating a key pair
First, the program prompts the user to enter two prime numbers (p and q), which are then stored as BigInteger variables. Large prime numbers can easily be generated using BigPrimes.org and should be at least 150 digits long. These values are used to calculate n, which is also represented as a BigInteger.
String pStr = Scanner1.next();
BigInteger pBig = new BigInteger(pStr);
String qStr = Scanner1.next(); // enter q
BigInteger qBig = new BigInteger(qStr);
BigInteger nBig = pBig.multiply(qBig);Next, φ(n) is calculated.
BigInteger nBigEuler = (pBig.subtract(BigInteger.ONE)).multiply(qBig.subtract(BigInteger.ONE));The program now prompts for the exponent e and stores it as BigInteger.
String eStr = Scanner1.next();
BigInteger eBig = new BigInteger(eStr);d is then calculated based on e and φ(n)
BigInteger dBig = eBig.modInverse(nBigEuler);Lastly, the user can choose the file names under which the keys will be saved. The program then stores the key values in two separate files at “(…)\user.dir\files” using the .json format.
In practice, RSA keys are not usually stored as raw {e, n} / {d, n} JSON, even though that representation is mathematically correct. In real-world systems, RSA keys are stored using standardized ASN.1 structures (PKCS#1 / PKCS#8 for private keys and X.509 SubjectPublicKeyInfo for public keys), encoded in DER binary and often wrapped in PEM (Base64 with headers), looking somewhat similar to this:
-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQC...
-----END RSA PRIVATE KEY-----However, for the purpose of this project, storing the key values in JSON format does the trick.
Generating a message
In the next step, the program prompts the user to enter a message and a filename.
String message = Scanner1.nextLine();
String filenameMessage = Scanner1.nextLine();Then, program saves the message under the specified file name in the “(…)\user.dir\files” directory.
try (FileWriter writerMessage = new FileWriter(new File(ordner, filenameMessage)))
{
writerMessage.write(message);
}Encrypting a message
To encrypt a message, the program first prompts the user to select which file to encrypt and which public key to use. It does so by scanning and listing all contents of the “(…)\user.dir\files” directory. The user can then choose the message file as well as the public key created earlier.
File ordner = new File(System.getProperty("user.dir") + "/Files");
File[] listFiles = ordner.listFiles();
int i = 1;
System.out.println("Your existing files are: ");
for (File file : listFiles) {
System.out.print(i + ") ");
System.out.println(file.getName());
i++;
}
String publicKeyFile = Scanner1.nextLine();
String contentMessage = Scanner1.nextLine();Next, the user is asked to choose a file name for the newly encrypted file.
String encryptedFilename = Scanner1.nextLine();The program then extracts the public key values as well as the content of the message. Next, the message content is converted into a decimal number, as described earlier. To achieve this, a loop goes over each character of the input message, converts it to its ASCII decimal value, and then transforms it into it’s 8-bit binary representation. Each binary segment is padded with leading zeros if necessary and appended to a StringBuilder, resulting in one continuous binary string.
int messageLength = contentMessage.length();
StringBuilder binaryString = new StringBuilder();
for (int j = 0; j < messageLength; j++) {
int messageAsciiValue = (int) contentMessage.charAt(j);
String binaryConvStr = Integer.toBinaryString(messageAsciiValue);
String paddedBinary = String.format("%8s", binaryConvStr).replace(' ', '0');
binaryString.append(paddedBinary);
}The Binary string is then converted into its decimal value.
BigInteger messageDecimal = new BigInteger(binaryString.toString(), 2);Finally, the encryption formula is applied, and the encrypted message is saved under the previously specified file name in the “(…)\user.dir\files” directory.
BigInteger ciphertext = messageDecimal.modPow(bigE, bigN);
try (FileWriter writerMessage = new FileWriter(new File(ordner, encryptedFilename)))
{
writerMessage.write(strCiphertext);
}
catch (IOException ex) {
}Decrypting a message
To decrypt a previously encrypted message, the program first prompts the user to select the file to decrypt and the private key to use. As before, it scans and lists all contents of the “(…)\user.dir\files” directory. The user can then choose the encrypted message file as well as the key file created earlier. The private key must be the corresponding counterpart to the public key that was used for encryption.
File ordner = new File(System.getProperty("user.dir") + "/Files");
File[] listFiles = ordner.listFiles();
int i = 1;
System.out.println("Your existing files are: ");
for (File file : listFiles) {
System.out.print(i + ") ");
System.out.println(file.getName());
i++;
}
String privateKeyFile = Scanner1.nextLine();
String encryptedMessage = Scanner1.nextLine();The user is once again prompted to choose a file name for the decrypted message file.
String decryptedFilename = Scanner1.nextLine();The program then extracts the private key values as well as the content of the encrypted message. It then uses the decryption formula to decrypt the message.
BigInteger decryptedMessageDecimal = ciphertextBig.modPow(bigD, bigN);This decimal number is then converted into a single binary string, as described earlier.
String decryptedMessageBinary = decryptedMessageDecimal.toString(2);The binary string is padded with leading zeros to the next multiple of eight to ensure correct conversion back into decimal values.
int remainder = decryptedMessageBinary.length() % 8;
if (remainder != 0) {
int padding = 8 - remainder;
decryptedMessageBinary = "0".repeat(padding) + decryptedMessageBinary;
}It’s then devided into 8-Bit groups (Octets).
List<String> groups = new ArrayList<>();
for (int l = 0; l < decryptedMessageBinary.length(); l += 8) {
groups.add(decryptedMessageBinary.substring(l, l + 8));
}Finally, the octets are converted back into their corresponding ASCII characters.
StringBuilder asciiString = new StringBuilder();
for (String group : groups) {
int decimalValue = Integer.parseInt(group, 2); // binary -> decimal
asciiString.append((char) decimalValue); // decimal -> ASCII char
}Lastly, the program creates a file containing the decrypted message using the previously specified file name and saves it in the “(…)\user.dir\files” directory.
String decryptedMessage = asciiString.toString();
try (FileWriter writerMessage = new FileWriter(new File(ordner, decryptedFilename))) {
writerMessage.write(decryptedMessage);
}
catch (IOException ex) {
}Final words
There is certainly a lot of room for improvement in the code, such as an automatic “random” prime number generator, additional checks for valid input, input sanitization, and proper error handling. Nothing that OpenSSL couldn’t do already. 😁
I had a lot of fun getting into this topic and working with it on a practical level. I am already looking forward to my next project involving cryptography – stay tuned!
